Given: Δ ABC with AC2 = AB2 +
BC2
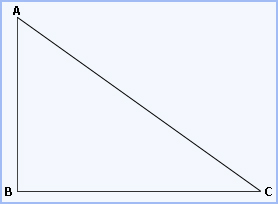
Prove:  ABC = 90°
ABC = 90°
 ABC = 90°
ABC = 90°Construction: We construct a right triangle PQR, such that PQ = AB, QR = BC and  PQR = 90°
PQR = 90°
 PQR = 90°
PQR = 90°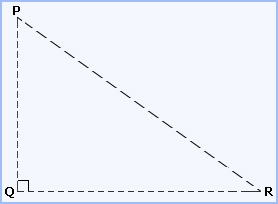
Proof:
In Δ PQR,  Q = 90°.
Q = 90°.
 Q = 90°.
Q = 90°.By Pythagoras
theorem, PQ2 + QR2 = PR2
From construction, AB2 + BC2 = PR2 ------ (1)
But, AB2 + BC2 = AC2 ----------- (2)
From (1) and (2),
we get: PR2 = AC2
we get: PR2 = AC2
 PR = AC.
PR = AC.By SSS criteria for congruence of triangles,
we get Δ ABC  Δ PQR.
Δ PQR.
 Δ PQR.
Δ PQR.
So that  B =
B =  Q = 90°.
Q = 90°.
 B =
B =  Q = 90°.
Q = 90°.