Basic Proportionality Theorem
Basic proportionality theorem (or) Thales theorem:
If a line is drawn parallel to one side of a triangle intersecting the other two sides then it divides these sides in the same ratio.
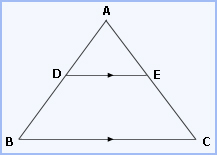
Given: A Δ ABC. A line DE is parallel to BC,
meeting AB at D
and AC at E.
To prove: AD/DB = AE/EC
Proof: From the figure ,
ABC and ADE we have
ABC =
ADE .......
(
Corresponding angles
are equal.)
ACB =
AED .......
( Corresponding angles
are equal.)
Then by AA axiom of similarity we can conclude that ABC ~ ADE
ABC ~ ADE We know that corresponding sides of a similar triangles are proportional.
| ∴ AB / AD | = | AC / AE |
| ⇒ ((AD + DB) / AD) | = | ((AE / EC) / AE) .... (∵ AB = AD + DB and AC = AE + EC) |
| ⇒ 1 + (DB / AD) | = | 1 + (EC / AE) |
| ⇒ (DB / AD) | = | EC / AE |
| ⇒ (AD / DB) | = | AE / EC .....(by taking reciprocals) |
| Hence, AD / DB | = | AE / EC |
Converse of Basic Proportionality Theorem:
If a line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side.
Given: A Δ ABC and DE is a line meeting AB in D and AC in E such
that AD / BD = AE / EC
To prove: DE || BC
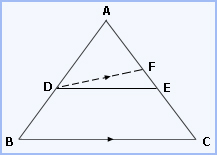
Proof: If possible let DE is not parallel to BC.
Then, draw DF parallel to BC AD / DB = AF / FC
| Given AD / DB | = | AE / EC |
| Now, we have AD / DB | = | AF / FC |
| and AD / DB | = | AE / EC |
| ⇒ AF / FC | = | AE / EC |
| By adding 1 on both sides, we can write | ||
| 1 + (AF / FC) | = | 1 + (AE / EC) |
| ⇒ ((AF + FC) / FC) | = | ((AE + EC) / EC) |
| ⇒ AC / FC | = | AC / EC ....... (∵ AF + FC = AC and AE + EC = AC) |
| ⇒ FC | = | EC |
Midpoint theorem:
The line segment joining the mid points of any two sides of a triangle is parallel to the third side and equal to half of it
Given: In a ΔABC, D and E are the mid-points of sides AB and AC
respectively
To prove:
(a) DE || BC
(b) DE = 
BC
BCConstruction: Through C, draw CF || BA, meeting DE produce at F
Proof:
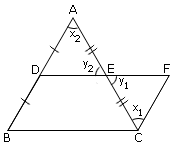
In Δ ADE and ΔCFE, with the notation in the figure.
| Statements | Reason |
|---|---|
| x1 = x2 | Alt. s , CF
|| BA. |
| y1 = y2 | Vertical opposite angles |
| CE = AE | Given E is the mid-point of AC |
 ΔCEF  ΔAED |
AAS axiom of congruency of Δs |
 CF = AD |
CPCT |
| But, AD = BD | Given, D is the mid-point of AB |
| CF = BD Also, CF
|| BD |
Construction |
| DBCF is a
||gm |
A pair of opposite sides are equal and parallel |
| DF || BC
|
Definition of a ||gm |
| i.e., DE || BC DF = BC | Opp. sides of a ||gm |
| Also, DE = EF | Congruency of Δs |
| DE = DF or DE = BC |
DF = BC |
Hence, DE || BC and
DE =
BC Q.E.D.
BC Q.E.D.Converse of Midpoint theorem:
The straight line drawn through the middle point of one side of a triangle parallel to another side bisects the third side.
Given: The mid–point D of the side AB and the line DE through D and
parallel to BC cutting AC at E
To prove: AE = EC
Construction: Draw CF || BA to meeting DE produced at F
Proof:
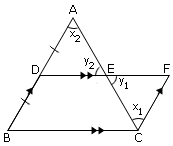
In Δ CEF and AED with the notation in the figure,
| Statements | Reason |
|---|---|
| DF || BC | Given |
| CF || BD | Construction |
| DBCF is a || gm
|
Definition of a || gm |
| CF = BD |
Opp. sides of a || gm |
| But, BD = DA | Given |
| CF = DA |
x1 = x2 | Alt. s ,
CF ||
BA. |
| y1 = y2 | Vertical opposite angles |
| CF = DA | Proved above |
| ΔCFE ΔADE
|
AAS axiom of congruency of Δs |
| CE = AE | CPCT |
Hence, E is the mid–point if AC Q.E.D.
Vertical angle bisector theorem:
The bisector of the vertical angle of a triangle divides the base in the ratio of the other two sides.
Given: In the ΔABC the bisector of BAC intersects BC at D
BAC intersects BC at DTo prove: BD / DC = AB / AC
Construction: Draw CE || DA to meet, BA produced in E.
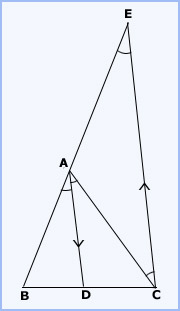
Proof: Since CE || DA
| CAD |
= | ACE
( Alternate
angles are equal) ------- (1)
|
| BAD |
= | AEC ( Corresponding
angles are equal) ------ (2) |
But given that BAD =
CAD
BAD =
CAD
From (1)
and (2) we get| ACE |
= | AEC |
| So, AC | = | AE ------- (3) |
By basic proportionality theorem in the BCE, DA
|| CE
BCE, DA
|| CE| ∴ BD / DC | = | BA / AE |
| Hence, by(3) we get | ||
| BD / DC | = | AB / AC |