EXAMPLES
1
Find the square root of 784?
Sol:
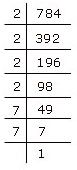
Square root of 784 by prime factorisation
Resolving 784 into prime factors, we get
784 = 2 × 2 × 2 × 2 × 7 × 7
= (2 × 2) × (2 × 2) × (7 × 7)
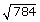= 2 × 2 × 7
= 28
Ex 2
Find the square root of 441?
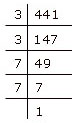
Square root of 441 by prime factorisation
Resolving 441 into prime factors, we get
441 = 3 × 3 × 7 × 7
= (3 × 3) × (7 × 7)
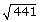= 3 × 7
= 21
Ex 3
Find the smallest number by which 2400 should be multiplied to get a perfect square number ?
Sol:
Square root of 2400 by prime factorisation
Resolving 2400 into prime factors, we get
2400 = 2 × 2 × 2 × 2 × 5 × 5 × 2 × 3
        = (2 × 2) × (2 × 2) × (5 × 5)
× (2 × 3)
Clearly, in the product of prime factors,
there are 3 pairs of equal factors and two factors 2 and 3 which do not exist in pairs.
So, we should multiply the given number by 2 × 3 = 6 to get a perfect square number.
Perfect square number so obtained = 2400 × 6 = 14400
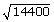= 2 × 2 × 5 × 2 × 3 = 120