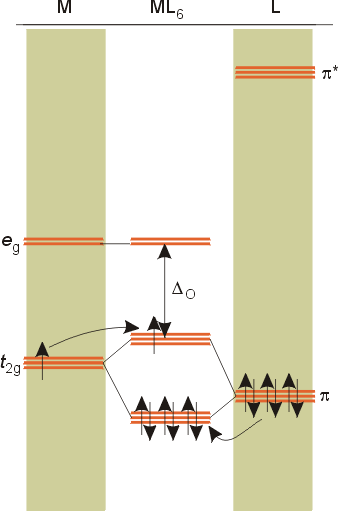
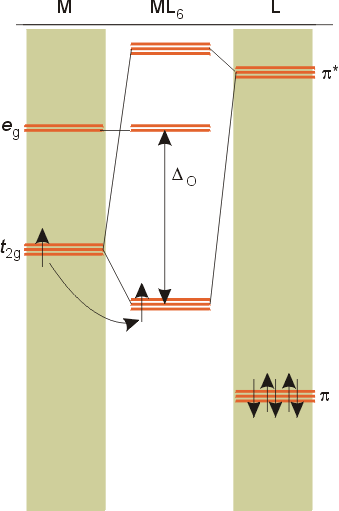
Overview of crystal field theory analysis
- The nature of the metal ion.
- The metal's oxidation state. A higher oxidation state leads to a larger splitting.
- The arrangement of the ligands around the metal ion.
- The nature of the ligands surrounding the metal ion.
- The stronger the effect of the ligands then the greater the difference between the high and low energy d groups.
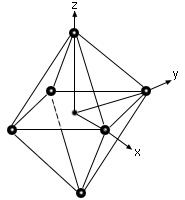
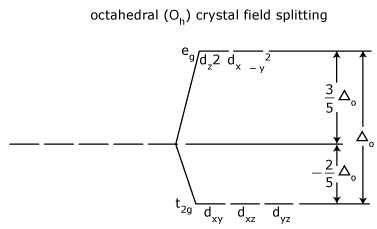
- The most common type of complex is octahedral; here six ligands form an octahedron around the metal ion.
- Nature Of Metal Ion
Arrangement Of Ligands Around The Metal Ion In Octahedral Crystal Field Splitting :
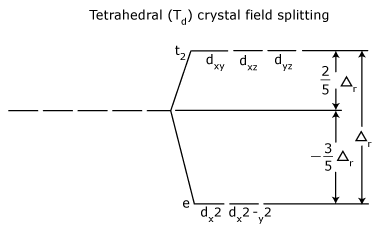
Tetrahedral Crystal Field Splitting
Square Crystal Field Splitting

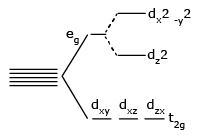
Jahn-Teller effect :
The expected effects for octahedral coordination are given in the following table:
| Number of d electrons | High spin | Low spin |
|---|---|---|
| 1 | w | w |
| 2 | w | w |
| 3 | ||
| 4 | s | w |
| 5 | w | |
| 6 | w | |
| 7 | w | s |
| 8 | ||
| 9 | s | s |
| 10 |
Nature of Ligands :
High-spin and low-spin Complexes :
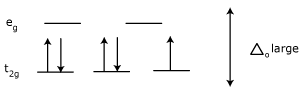
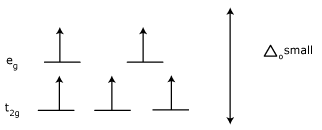
Effect on Magnetism :
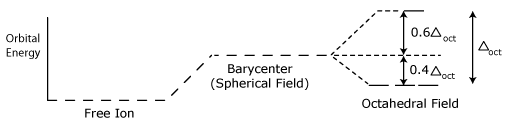
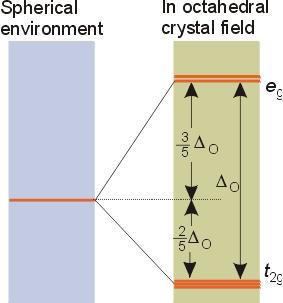
- The crystal field splitting energy for octahedral metal complexes (six ligands) is referred to as Δoct.
- The crystal field splitting energy for tetrahedral metal complexes (four ligands) is referred to as Δtet,
- The crystal field splitting energy for tetrahedral metal complexes (four ligands) is roughly equal to 4/9Δoct (for the same metal and same ligands).
The following are some of the High spin and Low spin complexes :
Crystal field stabilization energy
Ligand Field Theory
| Metal orbital | Symmetry label | Degeneracy |
|---|---|---|
| s | a1g | non-degenerate |
| px, py, pz | t1u | triply degenerate |
| dxy, dyz, dxz | t2g | triply degenerate |
| dx2 - y2, dz2v | eg | doubly degenerate |
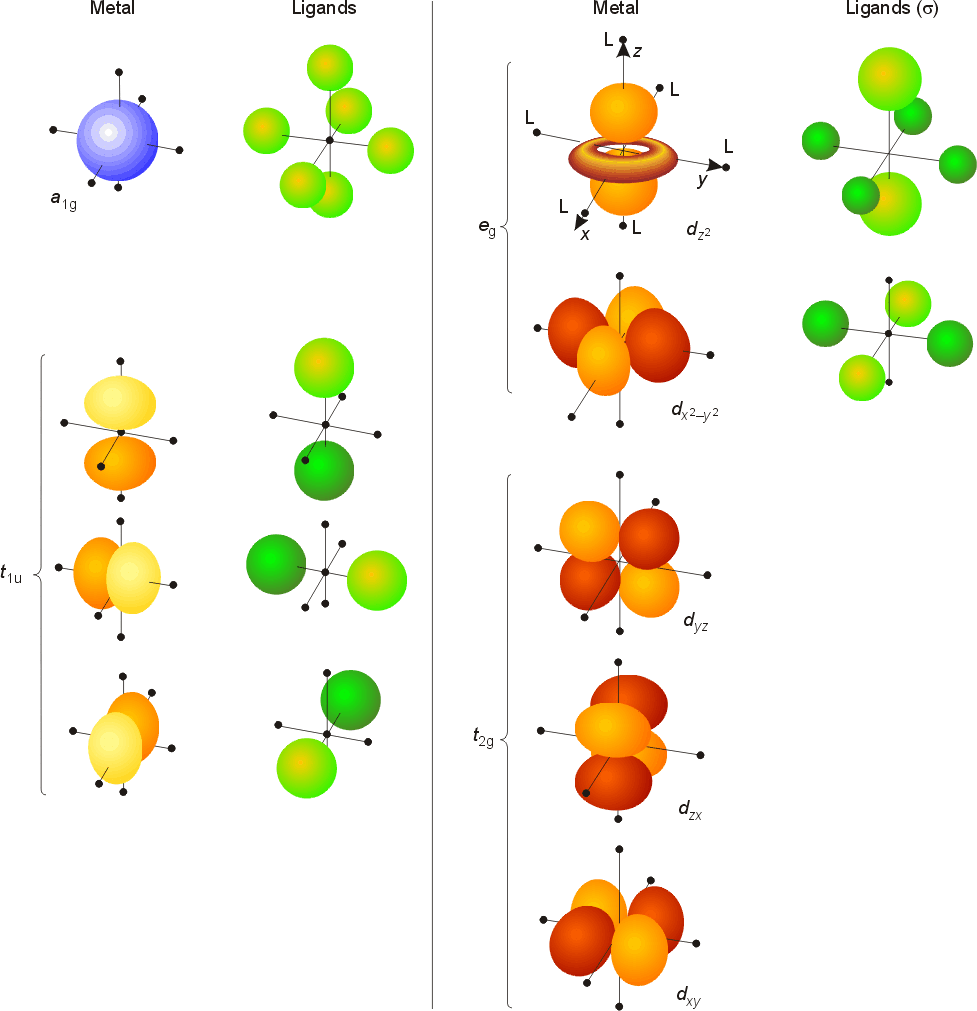
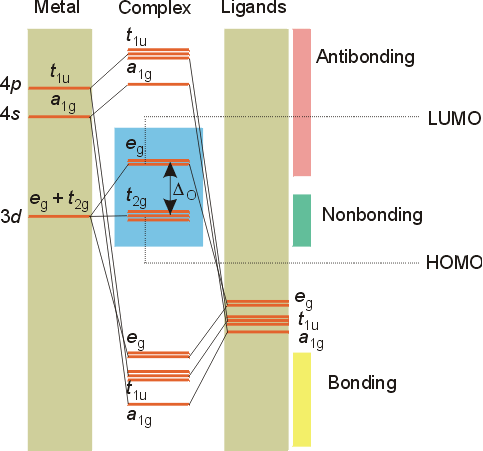
M.O diagrams
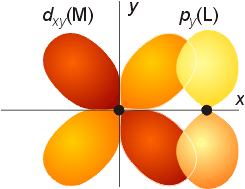
dπ - pπ bonding