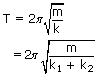A block of unknown mass is attached to a spring of spring constant 6.5 N/m and undergoes simple harmonic motion with an amplitude of 10cm. When the mass is halfway between its equilibrium position and the end point, its speed is 30 cm/s. Find the mass of the block and the time period of the motion ?
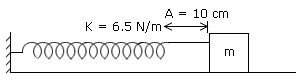
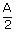 = 0.05m is v = 30 cm/s = 0.3 m/s
= 0.05m is v = 30 cm/s = 0.3 m/s| V | = | 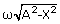
|
| ω2 | = | 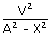
|
At x = 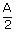 , v = 0.3 m/s , v = 0.3 m/s |
||
| ω2 | = | 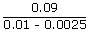
|
| = | 12 | |
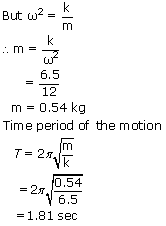
|
A mass M is attached to a spring. It oscillates every 2 sec. If the mass is increased by 5 kg, the period increases by 3 sec. Find the initial mass M, assuming that Hooke's law is obeyed.
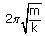
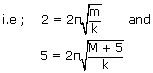
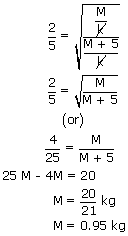
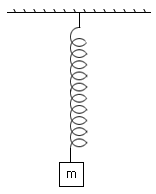
A mass m is oscillating freely on a vertical spring, when m = 0.81 kg , the period is 0.91 sec. An unknown mass on the spring has a period of 1.16 sec. Find the spring constant and the unknown mass?
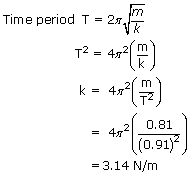
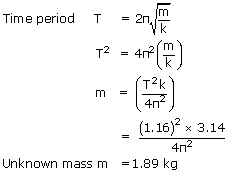
A body of mass 12 kg is suspended by a coil spring of natural length 50 cm and force constant 2 × 103 N/m. What is the stretched length of the spring ? If the body is pulled down further stretching the spring to 59 cm and then released, what is the frequency of oscillations of the suspended mass ?
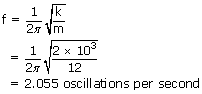
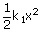
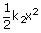
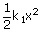 >
> 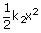
(ii) Let each spring is stretched by the same force, and x1 and x2 be the extension in each spring then
| x1 | = | 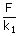
|
| x2 | = | 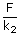
|
| work done on first spring | = | 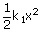
|
| = | 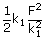
|
|
| = | 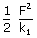
|
|
| work done on second spring | = | 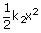
|
| = | 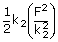
|
|
| = | 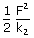
|
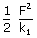 <
< 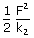
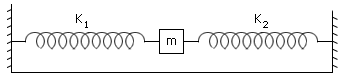
A block of mass m is placed on a frictionless surface and is connected to two springs of force constants k1 and k2. calculate the time period of the oscillation of the block?