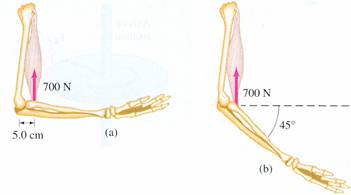
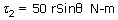The biceps muscle exerts a vertical force of 700N on the lower arm as shown below. Assume that the muscle is attached 5cm from the elbow. Calculate the torque about the axis of rotation through the elbow joint due to the weight of the lower arm and hand ?
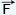 and the position vector
and the position vector
 (r = 5cm) is 45°
(r = 5cm) is 45°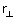 , inorder to calculate the torque.
, inorder to calculate the torque.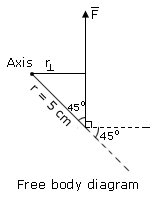
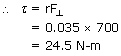
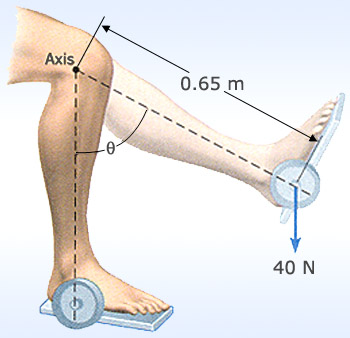
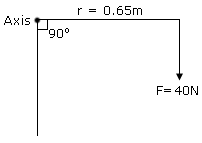
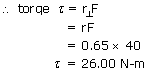
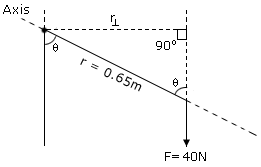
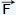 and the position vector
and the position vector
 is also θ(r is a transversal intersecting two parallel lines)
is also θ(r is a transversal intersecting two parallel lines)
One end of a rod is hinged to a table, so that the rod can rotate freely on the table top.Two forces, both parallel to the table top, act on the rod at the same place. One force is directed perpendicular to the rod and has a magnitude of 30N. The second force has a magnitude of 50N and is directed at an angle θ with respect to the rod. Tf the sum of the torques due to the two forces is zero, what must be the angle θ?
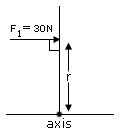
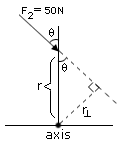
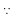 sinθ = sin 90 = 1)
sinθ = sin 90 = 1)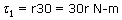
 τ2 =
τ2 =  ×
×
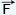 = r
= r F = (r sinθ)F
F = (r sinθ)F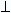 is the lever arm.
is the lever arm.