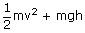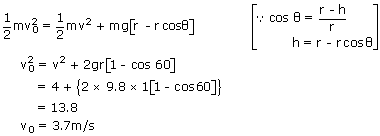Vertical Circular Motion
Q1

A roller coaster at an amusement park has a dip that bottoms out in a vertical circle of radius r. A passenger feels the seat of the car pushing upward on her with a force equal to twice her weight as she goes through the dip. If r = 20m, how fast is the roller coaster traveling at the bottom of the dip?

Sol:

Given radius of the vertical circle r = 20m
Let m be the mass of the passenger

At the bottom of the dip, the centripetal force is given by

Given that at the bottom of the dip the normal force FN (upward pushing force) is twice the weight of the passenger.

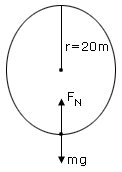
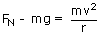
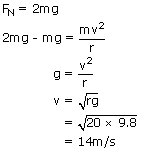
v = 14 m/s is the velocity of the roller coaster at the bottom of the dip.

Q2

A stone of mass 100 gm is suspended from the end of a weightless string of length 1m and is allowed to swing in a vertical plane. The speed of the stone is 2m/s when the string makes an angle of 60° with the vertical. Calculate the tension in the string at θ = 60°. Also find the speed of the stone when it is in the lowest position.

Sol:

Mass of the stone M = 100 gm = 0.1 kg
Radius of the circle r = 1 m
Speed of the stone at θ = 60°
v = 2 m/s

When the string is at an angle 60° with vertical, the weight can be resolved into rectangular components, and the centripetal force at this point is given by

Now to find the speed of the stone at the lowest position,
let us apply the principle of conservation of energy at the lowest point and at the point P
Energy at O = Energy at P
=
vo is the velocity at the lowest point O
v is the velocity at the point P where θ = 60°
given v = 2 m/s
vo = 3.7 m/s is the speed at lowest position.
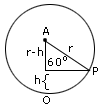
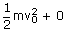