Atmospheric Pressure
Q1

The atmospheric pressure is 80 cm of Hg. Express it in N m–2 Use: density of Hg = 13.6 g cm–3, g = 9.8 m s–2?

Sol:
Given: h = 80 cm
= 0.8 m,
g = 9.8 m s−2
ρ = 13.6 g cm−3
= 13.6 × 103 kg m−3.
Atmospheric pressure P = h ρ g
= 0.8 × 13.6 × 103 × 9.8
= 10.662 × 104 N m−2
Q2

What length of water column is equivalent to 0.76 m of mercury column? State the assumption made in your calculation. Can water be used in a barometer? Give a reason.

Sol:

Let the density of mercury is 13.6 times the density of water.

h1 ρ1 g = h2 ρ2 g
(or) h2 = h1 ρ1/ρ2
= 0.76 × 13.6
= 10.34 m

Water can not be used in a barometer because it will then require the barometer tube of length more than 10.34 m which will be inconvenient.

Q3

A mercury barometer reads 70 cm. Now 3 cm3 of atmospheric air is introduced into the tube. The mercury falls to a height of 60 cm and the length of air column above the mercury is found to be 15 cm. Calculate the cross–sectional area of the barometer tube?

Sol:

Initially, the volume of air V1 = 3 cm3
Pressure P1 = atmospheric pressure = 70 cm of mercury
The mercury level falls to 60 cm because the air in the tube exerts pressure on it
therefore, pressure of the air inside tube P2 = 70 − 60 = 10 cm of Hg
Volume of the trapped air V2 = 15 × A
where A is the area of cross–section of the tube.

By Boyle's law, P1V1 = P2V2
70 × 3 = 10 × ( 15 × A)
∴A = (70 × 3) / (10 × 15)
= 1.4 cm2
Q4

Figure shows a mercury barometer tube of cross sectional area 1.8 cm2. Some air is trapped above the mercury column. Using the information given in the diagram, calculate the volume of the trapped air. If the atmospheric pressure is 76 cm of Hg, what is the pressure of trapped air ? On another occasion, the mercury level in the tube stands at 75 cm above the mercury level in the trough. Find the new volume of the enclosed air, the new pressure of the trapped air, and the atmospheric pressure?

Sol:
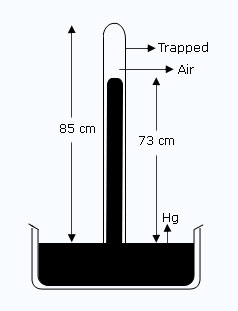
Initially the length of trapped air in the tube l = 85 – 73 = 12 cm.
Volume of the trapped air V1 = A × l
= 1.8 × 12
= 21.6 cm3
Pressure of the trapped air P1 = 76 – 73 = 3 cm of Hg.

On another occasion,
(i) The volume of the trapped air V2 = (85 – 75) × 1.8 = 18 cm3
(ii) Let the pressure of the trapped air be P2 cm of Hg

By Boyle's law, P1V1 = P2 V2
3 × 21.6 = P2 × 18
P2 = 3 × 21.6/ 18
= 3.6 cm of Hg

(iii) Atmospheric pressure P = 75 + 3.6 = 78.6 cm of Hg.

Q5

Some air has leaked into a mercury barometer tube (faulty barometer). The height of the mercury column is 75 cm and the length of the space above the mercury is 10 cm. When the tube is pushed further down into the mercury trough, the length of the space above the mercury is reduced to 5 cm and the height of mercury column is found to be 70 cm. Calculate the atmospheric pressure ?

Sol:

Let A be the cross sectional area of the tube and P be the atmospheric pressure.

Initial volume of the trapped air V1 = 10 × A cm3
And initial pressure P1 = (P – 75) cm of Hg
Final volume of the same air V2 = 5 × A cm3
And final pressure P2 = (P – 70) cm of Hg
By Boyle's law, P1 V1 = P2V2
(P – 75) × (10 × A) = (P – 70) × (5 × A)
or 2P – 150 = P – 70
∴ P = 150 – 70 = 80 cm of Hg.