Heating of electric currents

Ex 1:

An electric kettle is connected to 220 V mains supply. It took 5 minutes for the water in kettle to reach boiling point. How long would it take to boil the same amount of water, if the supply had been 120 V?

Sol:

The total electrical energy supplied to boil water in the kettle is W = VIt

Since nothing is clearly mentioned about the source of electrical power,

we assume that the power source is the same, that means the electrical energy obtained from the power source is the same,

i.e the current is same.

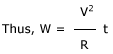
R is the resistance of the coil in the electric kettle.

We have to calculate t
The time t taken to boil the same amount of water for 120 V

supply is equal to

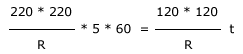
Solving this equation we get, t = 1008.33s = 16.8 minutes.

Ex 2:

A potential difference of 220 V is applied across a resistance of 1 kiloohm. Calculate the heat energy produced in 10 seconds.

Sol:

The heat energy produced can be calculated from

H = I²Rt joules.

Here I can be calculated from Ohm‘s law V = IR, V = 220V and R = 1 kiloohm

I=V/R=220/1000 = 0.22 A

From this H = 0.22 × 0.22 × 1000 × 10 = 484 J

Ex 3:

Calculate the temperature rise in 10 kg water when a 2 kW electric heater is switched on for 15 minutes. (Specific heat of water C = 4200J/kg/ ^oC).

Sol:

Power consumed by the electric heater P = 2 kW

Time t = 15 minutes = 15/60 hours = 0.25 hours

Heat energy H = P × t = 2 × 0.25 kW h = 0.5 kW h

Convert kWh to joules using the following equation:

1kW h = 3.6 × 10⁶ joules

0.5 kW h = 1.8 × 10⁶ joules

This is the energy used by the water heater to raise the temperature of water.

Heat used to raise the Temperature of water = Specific Heat of water (C) × Mass of water × Rise in Temperature ΔT

1.8 × 10⁶ joules = 10 kg × C × ΔT = 10 kg × 4200 J/kg/ ^oC × ΔT

⇒ ΔT = 42.85 ^oC

Thus the 10 kg of water will rise by 42.85^oC when a 2kW water heats it for 15 minutes.

Assuming the initial temperature of water is room temperature which is approximately 25^oC,

we can see the final temperature of the 19 kg water will be = 25^o C + 42.85^oC = 67.85^oC