Let P be any point on the ellipse. Draw PN perpendicular to the major axis and produce it to meet the auxiliary circle at Q. Then angle ACQ is called the ‘eccentric angle’ of the point P. Let us denote the angle as θ. If P starts from A and moves along the ellipse in the anti-clock wise direction and comes once again at A, then θ will vary from 0 to 2π.
Let the coordinates of P be (x, y).

Then x = a cos θ
[∵ from Δ CNQ, cos θ = x/a where CQ is the radius of the auxiliary circle]
Since P lies on the ellipse 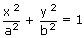 ,
,
we have 
| ⇒ y2 | = | b2 (1 – cos2 θ) |
| = | b2 sin2 θ | |
| ⇒ y | = | b sin θ |
∴ The coordinates of P are (a cos θ, b sin θ).
The point (a cos θ, b sin θ) is, for the sake of brevity, called the point θ and is denoted by P(θ).
If we put x = a cos θ, y = b sin θ in the equation of the ellipse, the equation is satisfied for all values of θ. Hence the pair of equations x = a cos θ, y = b sin θ together yield the single equation 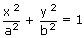 .
.
The two equations x = a cos θ, y = b sin θ are known as the parametric equations of the ellipse and 'θ' is called the parameter.

