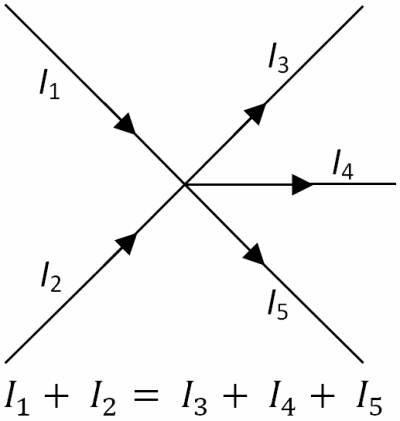
KCL
The currents going in to the node are equal to the currents coming out of the node.
Gustav Kirchhoff first described two laws that became central to electrical engineering.
The laws were generalized from the work of Georg Ohm. The laws can also be derived from Maxwell's
equations, but were developed prior to Maxwell's work.
The following descriptions of Kirchhoff's Laws assume a constant current. For time–varying current, or alternating
current, the laws must be applied in a more precise method.
(1) Kirchoff's current law
(2) Kirchoff's voltage law
Kirchoff's Current Law: This fundamental law results from the conservation of charge. It
applies to a junction or node in a circuit — a point in the circuit where charge has several possible paths to travel. Once
charge has entered into the node, it has no place to go except to leave (this is known as conservation of charge). The total
charge flowing into a node must be the same as the the total charge flowing out of the node. So, the sum of all the currents is
zero.
Note the convention we have chosen here: current flowing into the node are taken to be negative, and currents flowing out of the
node are positive.
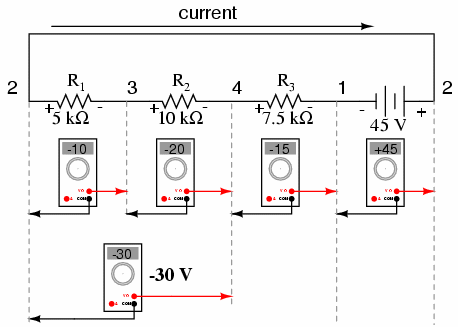KVL
When going from negative to positive (– to +) the voltage goes up, so the value is positive and vice
versa.
Kirchoff's Voltage Law: Kirchhoff's Voltage Law (or Kirchhoff's Loop Rule) is a result of the electrostatic field being conservative. It states that the total voltage around a closed loop must be zero. If this were not the case, then when we travel around a closed loop, the voltages would be indefinite.
We can adopt the convention that potential gains (i.e. going from lower to higher potential, such as with an emf source) is taken to be positive. Potential losses (such as across a resistor) will then be negative.
When traveling from positive to negative (+ to –) in an emf (power source) the voltage drops, so the value is negative. When going from negative to positive (– to +) the voltage goes up, so the value is positive. When crossing a resistor, the voltage change is determined by the formula I×R, where I is the value of the current and R is the resistance of the resistor. Crossing in the same direction as the current means the voltage goes down, so its value is negative. When crossing a resistor in the direction opposite the current, the voltage value is positive (the voltage is increasing).