Greek letter Psi
Psi is the 23rd letter of the Greek alphabet and has a numeric value of 700. The letter psi is commonly used in physics for representing a wave function in quantum mechanics. It is also used in biochemistry, pharmacology and computational theory. The Greek alphabet has an important role in the nomenclature of astronomical bodies and subatomic particles.
Wave function is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Probability amplitude is a complex number whose modulus squared represents a probability or probability density. The values taken by a normalized wave function Ψ at each point x are probability amplitudes, since | Ψ(x) | 2 gives the probability density at position x. The values of a wave function are complex numbers and, for a single particle, it is a function of space and time. The laws of quantum mechanics (the Schrodinger equation) describe how the wave function evolves over time. The wave function behaves qualitatively like other waves, like water waves or waves on a string. The most common symbol for a wave function is ψ (psi). Although ψ is a complex number, | ψ | 2 is real, and corresponds to the probability density of finding a particle in a given place at a given time, if the particle's position is measured.
In the classic double–slit experiment where electrons are fired randomly at two slits, an intuitive interpretation is that P (hit either slit) = P (hit first slit) + P (hit second slit), where P (event) is the probability of that event. However, it is impossible to observe which slit is passed through without altering the electron. Thus, when not watching the electron, the particle cannot be said to go through either slit and this simplistic explanation does not work. However, the complex amplitudes taken by the two wave functions which represent the electron passing each slit do follow a law of precisely the form expected Ψ (total) = ψ (first) + ψ (second), and the calculations agree with experiment.
Erwin Schrodinger (1887–1961)
Austrian physicist, Schrodinger is best known for his work on atomic structure. In 1926, Schrodinger published a series of papers that founded the science of quantum wave mechanics. His wave equation described the wave–like dual behavior of particles, and correctly predicted the electron distribution of the hydrogen atom. He shared the 1933 Nobel Prize for physics with Paul Dirac. He was physics professor at Berlin University from 1927–1933.
Schrodinger equation :
The most general form of the Schrodinger equation is the time–dependent
equation, which gives a description of a system evolving with time.
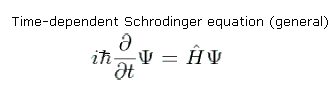
Where ψ is the wave function of the quantum system, i is the imaginary unit ħ,is the reduced Planck constant), and H is the Hamiltonian operator, which characterizes the total energy of any given wave function and takes different forms depending on the situation.
Schrodinger's cat
Showing a cat both dead and alive inside a blue box.
A quantum event (such as the decay of a radioactive particle) will trigger an event that will kill the cat, but because the box is sealed it is not known whether the quantum event has taken place or not. In this hypothetical situation, the cat is thought to be both alive and dead until observed. This is because according to quantum physics, a quantum event exists in an intermediate ‘probabilistic’ state until it is observed. This thought experiment was devised in 1935 by the Austrian physicist Erwin Schrodinger.
The non–relativistic Schrodinger equation for a single particle moving in an electric field is:
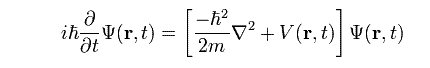
where m is the particle's mass, V is its potential energy,
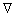
is the Laplacian operator, and ψ is the wave function (more precisely in this context, it is called the “position–space wave function”). In words, this equation could be described as “total energy equals kinetic energy plus potential energy”. Since differential operators are involved, this is a linear partial differential equation. It is also a wave equation, hence the name “Schrodinger wave equation”. The term “Schrodinger equation” can refer to both the general equation and the specific non relativistic version. The general equation is indeed quite general, used throughout quantum mechanics, for everything from the Dirac equation to quantum field theory, by plugging in various complicated expressions for the Hamiltonian. To apply the Schrodinger equation, the Hamiltonian operator is set up for the system, accounting for the kinetic and potential energy of the particles constituting the system, then inserted into the Schrodinger equation. The resulting partial differential equation is solved for the wave function, which contains information about the system.