The angles of a triangle are in the ratio 1 : 2 : 7. Show that the ratio of the greatest side to the least sides is (√5 + 1) : (√5 – 1).
Let the angles of the triangle be x°, (2x)° and (7x)°.
Then x + 2x + 7x = 180°
⇒ x = 18°
So, the angles are A = 18°, B = 36° and C = 126°.
Clearly, the least side is 'a' and the greatest side is 'c'
From the sine rule,
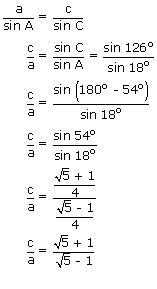
Hence c : a = (√5 + 1) : (√5 – 1)
The sides of the triangle are 3 consecutive natural numbers and its largest angles is twice the smallest one. Find the sides of the triangle.
Let a = x – 1, b = x, c = x + 1
Given C = 2A
From sine rule,
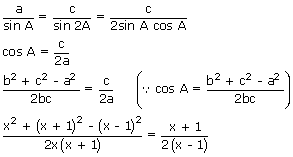
(x2 + 4x) 2(x – 1) = (x + 1)2 (2x)
x(x + 4) (x – 1) = (x + 1)2(x)
x2 – x + 4x – 4 = x2 + 2x + 1
x2 + 3x – 4 – x2 – 2x – 1 = 0
x – 5 = 0
x = 5
∴ The sides of the triangle are 4, 5, 6.
If b = 4 cms, ∠A = 45°, ∠B = 30° then find 'a'
from sine rule
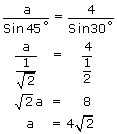
If a cos A = b cos B then prove that the triangle is either isosceles (or) right angled.
Given a cos A = b cos B
2R sin A cos A = 2R sin B cos B
sin 2A = sin 2B
⇒ sin 2A = sin 2B (or) sin 2A = sin(180 – 2B)
⇒ 2A = 2B (or) 2A = 180° – 2B
⇒ A = B (or) A + B = 90°
⇒ A = B (or) C = 90°
∴ The triangle is Isosceles (or) right angled.
Show that (b – a) cosC + c(cosB – cosA) = 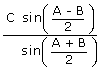
| LHS | = | (b – a) cos C + c(cos B – cos A) |
| = | (b cos C + c cos B) – (a cos C + c cos A) | |
| = | a – b | |
| = | 2R (sin A – sin B) | |
| = | 2R 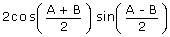 |
|
| = | 2R . 2sin C/2 . 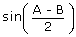 |
|
| = | 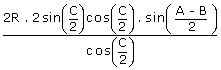 |
|
| = | 2R sinC 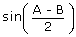 |
|
| = | 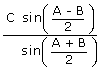 |
|
| = | RHS |